Bạn có nhớ cảm giác hồi hộp khi bước vào lớp 7, những kiến thức mới như một cánh cửa kỳ diệu mở ra? Chương 1 – Số hữu tỉ là bước khởi đầu đầy thú vị cho hành trình khám phá toán học của chúng ta. Để giúp bạn củng cố kiến thức và tự tin hơn trong học tập, bài viết này sẽ chia sẻ 10 Câu Hỏi ôn Tập Chương 1 Toán 7, cùng với những lời giải chi tiết và bổ ích.
1. Khái niệm số hữu tỉ
1.1. Số hữu tỉ là gì?
Câu hỏi: Số hữu tỉ là gì? Nêu ví dụ về số hữu tỉ?
Giải đáp: Số hữu tỉ là số viết được dưới dạng phân số $frac{a}{b}$, trong đó $a$ và $b$ là các số nguyên và $b$ khác 0.
Ví dụ: $frac{1}{2}$, $-3$, 0,5, 2,1… đều là số hữu tỉ.
Lưu ý: Mọi số nguyên đều là số hữu tỉ vì có thể viết chúng dưới dạng phân số có mẫu số là 1. Ví dụ: -3 có thể viết là $frac{-3}{1}$.
1.2. Biểu diễn số hữu tỉ trên trục số
Câu hỏi: Làm sao để biểu diễn số hữu tỉ trên trục số?
Giải đáp: Để biểu diễn số hữu tỉ $frac{a}{b}$ trên trục số, ta chia đoạn thẳng đơn vị thành $b$ phần bằng nhau. Từ điểm 0, ta lấy $a$ phần về phía dương nếu $a$ dương và về phía âm nếu $a$ âm.
Ví dụ: Để biểu diễn số hữu tỉ $frac{3}{4}$ trên trục số, ta chia đoạn thẳng đơn vị thành 4 phần bằng nhau, rồi lấy 3 phần về phía dương.
1.3. So sánh số hữu tỉ
Câu hỏi: Làm sao để so sánh hai số hữu tỉ?
Giải đáp: Có nhiều cách để so sánh hai số hữu tỉ.
Cách 1: Quy đồng mẫu số: Ta quy đồng mẫu số hai phân số rồi so sánh tử số. Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Cách 2: Quy đồng tử số: Ta quy đồng tử số hai phân số rồi so sánh mẫu số. Phân số nào có mẫu số nhỏ hơn thì phân số đó lớn hơn.
Cách 3: Sử dụng tính chất: Nếu $frac{a}{b} < frac{c}{d}$ thì $a.d < b.c$ và ngược lại.
2. Cộng trừ nhân chia số hữu tỉ
2.1. Cộng trừ số hữu tỉ
Câu hỏi: Làm sao để cộng trừ hai số hữu tỉ?
Giải đáp: Muốn cộng trừ hai số hữu tỉ, ta quy đồng mẫu số rồi cộng trừ tử số.
Ví dụ: $frac{1}{2} + frac{3}{4} = frac{2}{4} + frac{3}{4} = frac{5}{4}$
2.2. Nhân chia số hữu tỉ
Câu hỏi: Làm sao để nhân chia hai số hữu tỉ?
Giải đáp: Muốn nhân hai số hữu tỉ, ta nhân tử số với nhau và mẫu số với nhau. Muốn chia hai số hữu tỉ, ta nhân số bị chia với nghịch đảo của số chia.
Ví dụ: $frac{1}{2} times frac{3}{4} = frac{1 times 3}{2 times 4} = frac{3}{8}$
$frac{1}{2} : frac{3}{4} = frac{1}{2} times frac{4}{3} = frac{2}{3}$
3. Lũy thừa với số mũ tự nhiên
3.1. Lũy thừa với số mũ tự nhiên là gì?
Câu hỏi: Lũy thừa với số mũ tự nhiên là gì?
Giải đáp: Lũy thừa với số mũ tự nhiên là tích của $n$ thừa số bằng nhau, trong đó $n$ là một số tự nhiên lớn hơn 1.
Ví dụ: $2^3 = 2 times 2 times 2 = 8$
3.2. Tính chất lũy thừa
Câu hỏi: Nêu các tính chất của lũy thừa với số mũ tự nhiên?
Giải đáp: Lũy thừa với số mũ tự nhiên có các tính chất sau:
- Tính chất 1: $a^m . a^n = a^{m+n}$
- Tính chất 2: $(a^m)^n = a^{m.n}$
- Tính chất 3: $(a.b)^n = a^n . b^n$
- Tính chất 4: $(frac{a}{b})^n = frac{a^n}{b^n}$ (với $b$ khác 0)
4. Thứ tự thực hiện phép tính
4.1. Thứ tự thực hiện phép tính là gì?
Câu hỏi: Thứ tự thực hiện phép tính trong biểu thức số hữu tỉ là gì?
Giải đáp: Thứ tự thực hiện phép tính trong biểu thức số hữu tỉ như sau:
- Thực hiện các phép tính trong ngoặc đơn trước.
- Thực hiện phép tính lũy thừa.
- Thực hiện phép tính nhân và chia theo thứ tự từ trái sang phải.
- Thực hiện phép tính cộng và trừ theo thứ tự từ trái sang phải.
Ví dụ: Tính giá trị biểu thức: $2 + 3 times 4 – 5^2$
- Bước 1: Tính $5^2 = 25$
- Bước 2: Tính $3 times 4 = 12$
- Bước 3: Tính $2 + 12 – 25 = -11$
4.2. Áp dụng thứ tự thực hiện phép tính để giải bài toán
Câu hỏi: Làm sao để áp dụng thứ tự thực hiện phép tính để giải bài toán?
Giải đáp: Khi giải bài toán, ta cần chú ý thứ tự thực hiện phép tính để tránh sai sót.
Ví dụ: Bài toán: Một người đi xe máy từ A đến B với vận tốc 40 km/h, sau đó đi tiếp từ B đến C với vận tốc 50 km/h. Biết quãng đường AB dài 60 km và quãng đường BC dài 80 km. Hỏi người đó đi hết cả hai quãng đường AB và BC trong bao lâu?
- Bước 1: Tính thời gian đi quãng đường AB: $t{AB} = frac{s{AB}}{v_{AB}} = frac{60}{40} = 1,5$ (giờ)
- Bước 2: Tính thời gian đi quãng đường BC: $t{BC} = frac{s{BC}}{v_{BC}} = frac{80}{50} = 1,6$ (giờ)
- Bước 3: Tính tổng thời gian đi cả hai quãng đường: $t{AB} + t{BC} = 1,5 + 1,6 = 3,1$ (giờ)
5. Bài tập ôn tập chương 1 toán 7
5.1. Bài tập trắc nghiệm
Câu hỏi: Hãy chọn đáp án đúng cho các câu hỏi trắc nghiệm sau:
Câu 1: Số nào sau đây là số hữu tỉ?
a) $sqrt{2}$
b) $pi$
c) $frac{1}{2}$
d) $sqrt{3}$
Câu 2: Số nào sau đây biểu diễn số hữu tỉ $frac{-3}{4}$?
a)
b)
c)
d) 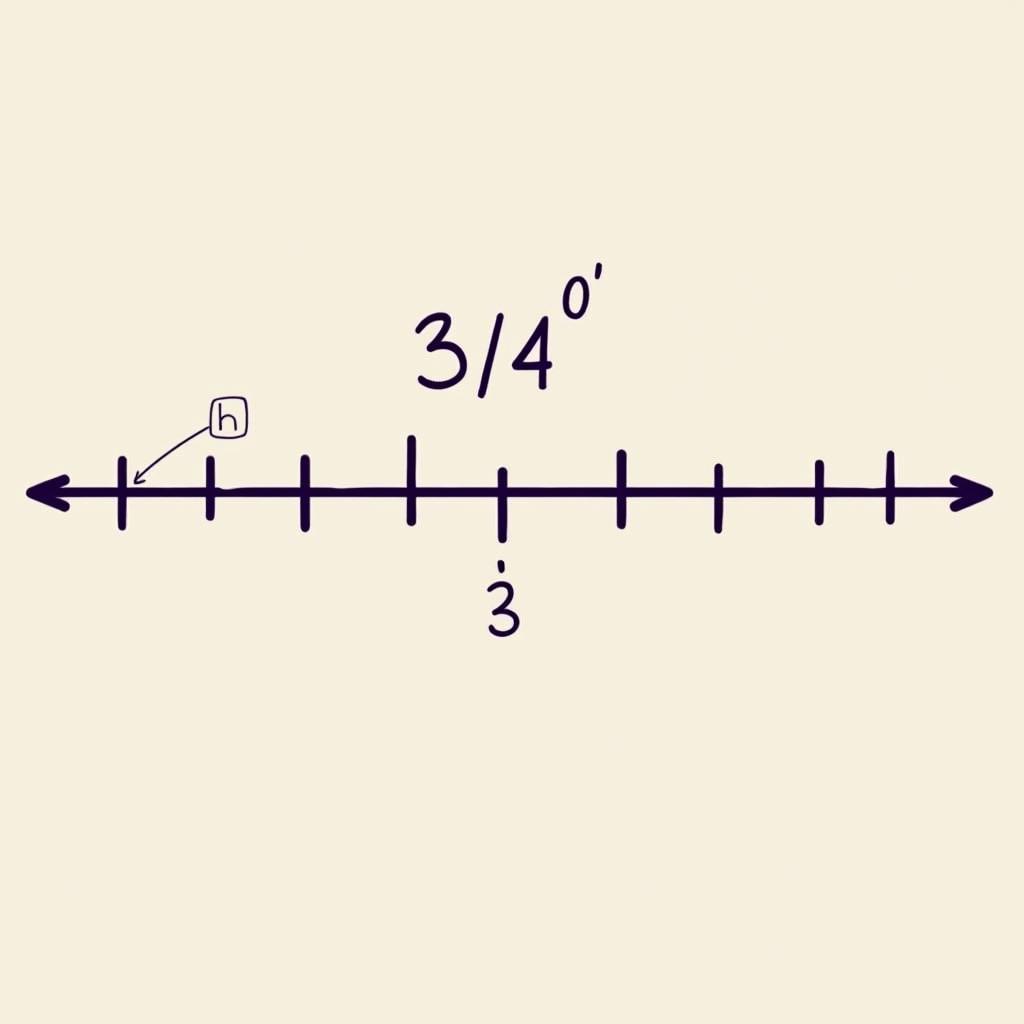 Biểu diễn số hữu tỉ -3/4 trên trục số
Biểu diễn số hữu tỉ -3/4 trên trục số
Câu 3: Kết quả của phép tính $frac{1}{2} + frac{1}{3}$ là:
a) $frac{2}{5}$
b) $frac{5}{6}$
c) $frac{1}{6}$
d) $frac{3}{5}$
Câu 4: Giá trị của biểu thức $2^3 – 3^2$ là:
a) 1
b) -1
c) 5
d) -5
Câu 5: Thứ tự thực hiện các phép tính trong biểu thức $2 + 3 times 4 – 5^2$ là:
a) Lũy thừa -> nhân -> cộng -> trừ
b) Cộng -> nhân -> lũy thừa -> trừ
c) Nhân -> cộng -> lũy thừa -> trừ
d) Lũy thừa -> cộng -> nhân -> trừ
5.2. Bài tập tự luận
Câu 1: So sánh hai số hữu tỉ sau:
a) $frac{2}{3}$ và $frac{3}{4}$
b) $frac{-1}{2}$ và $frac{1}{3}$
Câu 2: Thực hiện phép tính:
a) $frac{1}{2} + frac{1}{3} – frac{1}{4}$
b) $2^3 + 3^2 – 4^1$
Câu 3: Tính giá trị của biểu thức:
a) $frac{1}{2} times frac{3}{4} + frac{1}{3} : frac{2}{5}$
b) $2^3 + 3^2 times 4 – 5^2$
Câu 4: Một người đi xe máy từ A đến B với vận tốc 40 km/h, sau đó đi tiếp từ B đến C với vận tốc 50 km/h. Biết quãng đường AB dài 60 km và quãng đường BC dài 80 km. Hỏi người đó đi hết cả hai quãng đường AB và BC trong bao lâu?
6. Kết luận
Chương 1 – Số hữu tỉ là nền tảng cho các kiến thức toán học cao hơn. Việc nắm vững kiến thức chương này sẽ giúp bạn học tốt các chương tiếp theo. Hãy ôn tập thật kỹ những kiến thức đã học, luyện tập thật nhiều để củng cố kiến thức và tự tin chinh phục các bài kiểm tra. Hãy nhớ, “Học hành là gánh nặng ban ngày, nhưng là ánh sáng ban đêm”, chúc bạn học tốt và đạt kết quả cao!
Lưu ý: Để được hỗ trợ thêm, bạn có thể liên hệ với chúng tôi theo Số Điện Thoại: 0372899999, Email: [email protected] Hoặc đến địa chỉ: 233 Cầu Giấy, Hà Nội. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7, luôn sẵn sàng hỗ trợ bạn!